1.用途
现实是我们的处理和测量模型都是非线性的,结果就是一个不规则分布,KF能够使用的前提就是所处理的状态是满足高斯分布的,为了解决这个问题,EKF是寻找一个线性函数来近似这个非线性函数,而UKF就是去找一个与真实分布近似的高斯分布。
- KF处理线性模型:
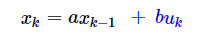
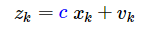
- EKF 通过雅克比和偏导数近似非线性模型,但是忽略了高阶导数:(强非线性系统下误差大,另一方面Jacobian矩阵的计算复杂)

- UKF 通过去点的方式近似非线性模型,因为没有用雅克比和偏导数,让计算变得更加简单,同时也没有忽略高阶导数项。
- PF不一定限于高斯分布
2.KF
卡尔曼滤波是一种高效率的递归滤波器(自回归滤波器), 它能够从一系列的不完全包含噪声的测量(英文:measurement)中,估计动态系统的状态,然而简单的卡尔曼滤波必须应用在符合高斯分布的系统中。
百度百科是这样说的,也就是说卡尔曼滤波第一是递归滤波,其次KF用于线性系统。
但经过研究和改进,出现了很多卡尔曼,如EKF(extended kalman filter)扩展卡尔曼,UKF(Unscented Kalman Filter)无迹卡尔曼等等。
而我们就来研究EKF,而EKF的中心思想就是将非线性系统线形化后再做KF处理。
状态方程
当我们从最简单的系统开始,我们假定k时刻的系统状态与k-1时刻有关,于是我们可以得到方程:
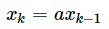
其中a为常量,但是当系统内部有噪声,我们称为过程噪声 ,计为w。所以方程可以写成:
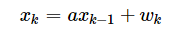
而我们实际观测的时候会出现观测噪声,于是我们将观测值计为Z,观测噪声为v,那我们可以把k时刻的观测值与系统状态值写成方程:
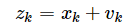
于是最简单的系统状态方程就有啦。
卡尔曼滤波算法核心思想在于预测+测量反馈,它由两部分组成,第一部分是 线性系统状态预测方程,第二部分是 线性系统观测方程。
这里系统的预测时候,我们要将通过系统状态方程计算的预测值作为先验信息,之后在观测部分在重新更新这个信息。
回头说状态的预测,我们引入一个符号 ^在相应的变量上表示该变量是预计值。再说一个新概念:新息。一个时间序列{X(t)}里,根据历史数据的预测值,新息是真实值减去预测值。
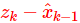
注:上有波浪线表示新息,也有用字母e表示的;上面尖的是预测值;无标注为真实值
我们给出一个优化过的预测值,新预测值 = 上一轮预测值(先验) + 权重 × 新息,即:
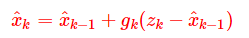
那下一个问题就是权重g是怎么计算得出的呢?答案是间接的从噪声里求得的。当我们将估计协方差叫做p,而传感器的协方差为r,我们通过这两个值计算权重。

既然获得了g,我们下一步将先验信息输入到上面的两个方程中获得后验预测值,也就是我们的输出值。
那整个计算步骤和过程就应该是这样的:

先预测后更新。具体计算过程和曲线生成可以参考的Part7。
之后我们再说更复杂一点的系统,系统地状态方程引入了输入量U。换句话说有一个U会时刻影响系统状态量。
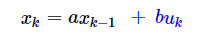
而观测到的观测值为
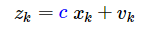
那我们新的计算方法就需要引入这两个新的变量,

同样是预测,更新,预测下一时刻,更新的计算方式。
而当系统用矩阵的方式写的状态方程,就需要以矩阵的方式计算。相同的数学公式及计算方法。如P的计算,
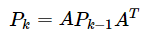
又如G,
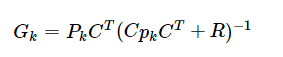
还有P的更新,
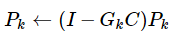

这样的话,我们的系统方程及计算步骤方式如下

需要注意的是我们使用的R是对测量误差v的协方差,当我们在引入一个Q代表过程噪声引起的误差时,可以使系统表现更好,即使Q很小,
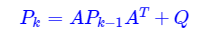
2.1 非线性系统之EKF
那如果系统是非线性的呢?我们如果将观测值Z计做X的非线性函数组成的,我们的模型可以改成。
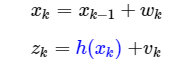
而我们的中心思想是将其线性化,如果我们使用函数一阶导为C来计算G和P。

最后系统复杂到这样的程度,

那我们就引入雅科比矩阵,雅各比矩阵就是方程矩阵对每一个变量的偏导数。
则在向量分析中,雅可比矩阵Jacobian matrix是该函数的所有分量( 个)对向量
的所有分量(
个)的一阶偏导数组成的矩阵。
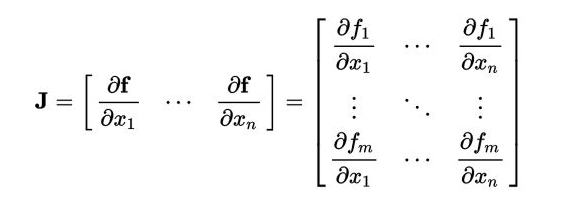
函数有 个分量,于是有
行。向量
有
个分量,于是有
列。
而最终,F为f方程的雅可比,H为h方程的雅可比。最终计算如下:
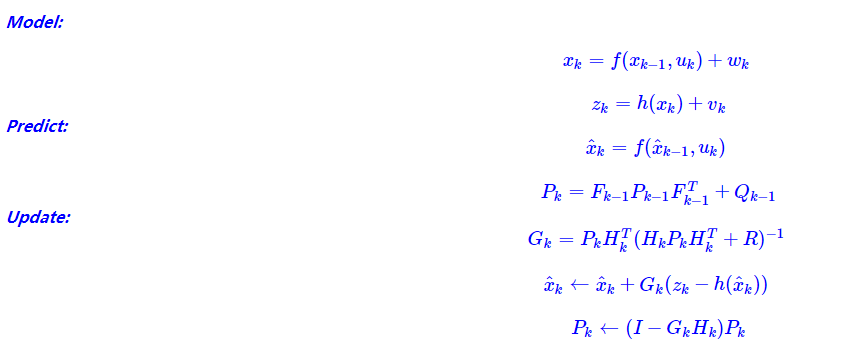
到这里简单的EKF就已经完成基本介绍啦。
3.UKF
3.1 模型
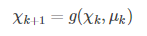
z(k+1)=h(x(k+1))
3.2 预测
1.预测sigma point(k+1步的分布点)
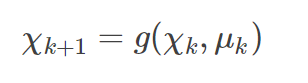
2.预测均值(Xpred)和方差(Ppred)
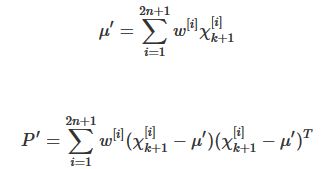
其中:
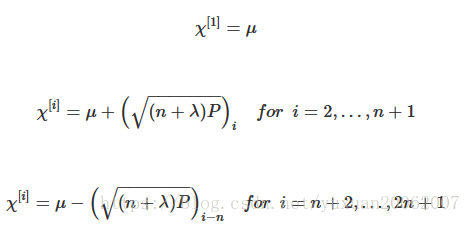
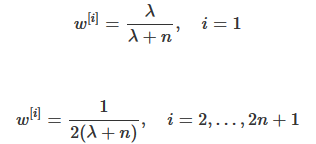
3.预测测量值
z(k+1)i=h(x(k+1)i)
从而zpred:
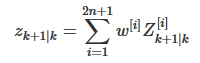
3.3更新
1.更新卡尔曼系数
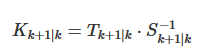
其中:
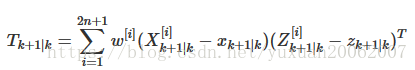

2.更新最终值: